この記事は、大学1、2年生レベルの力学を知っていることを前提に書いています。重要だと思った部分は太字で、数式や専門用語をなるべく使わずに書いているので、一般の方は太字だけ読むことをお勧めします。
打球後のボールについて
衝突後のボールの軌道を決める要素のうち、プレイヤーが直接コントロールできるのは以下の2つだけである。それ以外の影響は、空気やコートなどの周囲の環境によって左右される。
- ボールの進行方向と速度の大きさ（速度ベクトル）
- ボールの回っている向き（回転軸）と回転量
この2つがどのように決まるかを考え、意識すべきことを整理する。
速度の大きさ
まずは、速度の大きさについて考える。以下のような2次元平面の状況を設定し、衝突後のボールの速度v’を求める。衝突は、人+ラケットとボールの衝突のため、画像の棒は、ラケットだけでなく、人とラケットが合体したものとする。
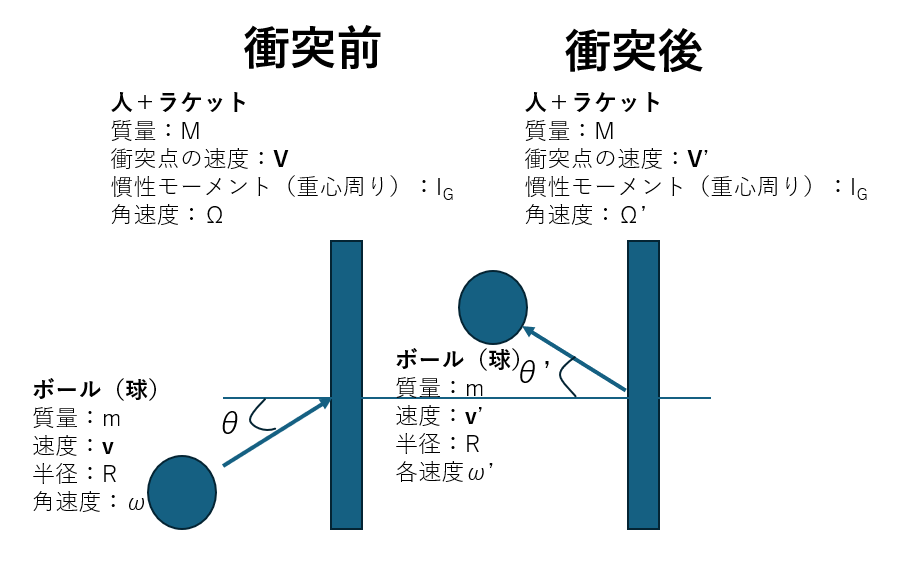
ここでは簡単のため、θ=0で考える。
・運動量保存の式
\[mv+MV=mv’+MV’\]
・反発係数
\[e=\frac{v’-V’}{V-v}\]
この2つの式から、衝突後のボールの速度は
\[v’=\frac{mv+MV+Me(V-v)}{M+m}\]
となる。
テニスボールの質量 m=60 g、衝突前のボールの速度 v=30 km/h、衝突前のラケットの速度 V=70 km/h として、縦軸v’、横軸Mでプロットしてみる。
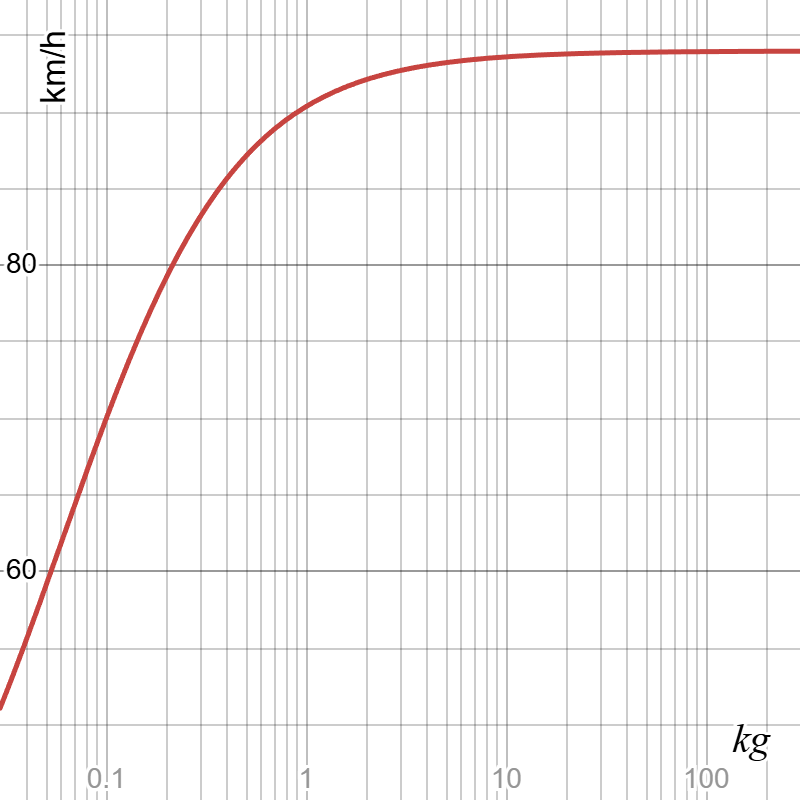
この結果から、なるべく大きな質量=体全体で衝突したほうが、早い速度でボールを飛ばせることがわかる。だいたいM=10 kgくらいで、v’は頭打ちになる。
仮に衝突直前に手の力を緩め、ほとんどラケットの質量（M＝300 g）だけの衝突になると、体全体で衝突した場合に比べて、10 km/h 近く速度を損する。
つまりインパクトの直前では、大きな質量で衝突するため、体をなるべく一体化させる必要がある=各関節が動かないように力をいれる必要がある。さらに、ボールがラケットに接触している数ミリ秒の間、ボールの勢いに負けて一体化が解けないように、ボールを押すようにする必要がある。
注意すべきは、関節を固めると運動連鎖を妨げラケットが加速しずらくなるため、インパクト直前以外にむやみに力をいれないこと（別の記事で解説）。
ボールの進行方向
θが0出ないときのvxを求める。x方向の運動量保存の式は、
\[mvcosθ+MV_{x}=mv’cosθ+MV_{x}’\]
反発係数は以下のように書ける。
\[e=\frac{v’cosθ’-V_{x}’}{V_{x}-vcosθ}\]
摩擦がない場合、
\[v’_{y}=vsinθ\]
\[V’_{y}=V_{y}\]
である。(4)、(5)、(6)より、ボールの衝突後の速度v‘は、次のように書ける
\[\mathbf{v’}=\begin{pmatrix}\dfrac{(m-eM)vcosθ+(1+e)MV_{x}}{m+M}\\\rule{0pt}{3.0ex}{vsinθ}\end{pmatrix}\]
従って、衝突後の角度θ’は、
\[θ’=arctan\left(\dfrac{(m+M)vsinθ}{(m-eM)vcosθ+(1+e)MV_{x}}\right)\]
となる。ラケットの速度がボールの速度より十分早いとき、θ’は0°になる。つまり、ラケットの速度がボールの速度に対して十分早いとき、ラケット面に対してほぼ垂直の方向にボールが飛び出す。従ってサーブやストロークでは、面の向きにボールが飛んでくれる。
逆にボールの方がラケットより早いときつまり、Vx <<vの時、M>>mとすると、式（9)は、
\[θ’=arctan\left(\dfrac{-1}{e}tanθ\right)\]
となる。e=0.6、θ=30°を代入してみると、θ’≒-43°となる。早い球をボレーするとき、入射角=反射角だと思って面を作ると、ボールが浮いてしまうわけだ。
ここまでの議論ではボールの回転を考慮していないことに注意。
ボールの回転とラケットの角度
打球に回転がかかるのは、ラケットとボールのインパクト時にストリングがずれ、その後、ストリングが元の位置に戻ろうとする力によってボールに回転が与えられるためである。この現象は「スナップバック」と呼ばれる。参考動画：
つまりストリングを大きく動かすほど、多くボールに回転をかけられると考えられる。ストリングを大きく動かすには、ボールをラケットになるべく食い込ませるのと同時にこする必要がある。つまり、回転量は、ラケットとボールの法線方向（食い込ませる方向）の相対速度が大きいほど、接線方向（こする方向）の相対速度が大きいほど増えると考えられる。
このスナップバックで、ボールに与えられるy方向の力積を$J_{t}$とする。$J_{t}$は、ボールの角運動量の変化量は、RJtなので、衝突後の回転速度ω’は、
\[ω’=ω+\frac{2J_{t}}{3mR}\]
となる。この時、運動量保存則より、$v’_{y}=v_{y}-J_{t}/m$となるので、衝突後のボールの速度$\bf{v’}$は式(8)から以下のように変わる。
\[\mathbf{v’}=\begin{pmatrix}\dfrac{(m-eM)vcosθ+(1+e)MV_{x}}{m+M}\\\rule{0pt}{3.0ex}{vsinθ-\frac{J_{t}}{m}}\end{pmatrix}\]
従って、$θ’$は、
\[θ’=arctan\left(\dfrac{(m+M)(vsinθ-\frac{J_{t}}{m})}{(m-eM)vcosθ+(1+e)MV_{x}}\right)\]
さらに、m<<Mのとき、式(13)は、
\[θ’=arctan\left(\dfrac{vsinθ-\frac{J_{t}}{m}}{(1+e)V_{x}-evcosθ}\right)\]
となる。例えばトップスピンの場合、$J_{t}$が大きいほど=回転量が多いほど、ボールはラケット面より上向きに飛び出す。このため、インパクト時にはラケット面を地面に対して垂直よりもやや伏せる必要がある。
Choppin et al. (2011)によると、熟練者は地面対して垂直よりも平均21°ラケット面を伏せてインパクトしているという。試しに、式(13)にKwon S et al. (2017)の実験結果のパラメータをいれてみる。以下のようにパラメータを代入するとθ’は、およそ-3.1°になり、地面に並行よりもやや上向きにボールが飛ぶという結果になった。
- e=0.8(参考)
- $V_{x}$=15.4 m/s (Kwon S et al. (2017) Table. 1)
- $J_{t}$=0.13 N・s（スピン量969 RPMから算出）
- θ=10° (Kwon S et al. (2017) Table. 1 ラケットの伏せ角)
- m=60 g
- v=5 m/s (Kwon S et al. (2017) Table. 1 では、球出しマシーンで11 m/sの速度のボールを出している。被験者がボールを打つ頃にはこれくらいになっていると仮定した。)
衝突時のラケットのブレについて
ラケットとボールの接触時間は、数ミリ秒である。この数ミリ秒の間、ラケットはボールから力積を受けラケットの面の角度などがずれ続ける。このブレが大きいと、打球のコントロールが難しくなる。このブレを小さくするにはどうすればよいか？
ラケットの衝突前と衝突後の、速度と回転速度の変化を計算する。この変化が大きいほど、ブレが大きくなる。
回転速度の変化は、式(11)同じようにして、重心から接触点の距離をdとすると、
\[Ω’-Ω=\frac{dJ_{t}}{I_{g}}\]
と書ける。この式から、以下のことが言える。
- dが大きいほど、変化が大きくなる。例えば手が長く、接触点の重心からの距離が大きいとブレが大きくなる。
- $J_{t}$が大きいほど、変化が大きくなる。回転をかけやすいラケットのほうが、ブレが大きくなる。
- ラケットと体全体の慣性モーメント $I_{G}$ が大きいほど、ボールが当たったときにラケットはぶれにくくなる。体重が重い人ほど、また当たる位置に近い部分の質量が大きいほど、ラケットは安定する。そのため、ラケットを重くすると打球時のブレは小さくなる。しっかり振れる範囲でなるべく重いラケットを使うのがブレを軽減するにはよいと言える。
衝突後ラケットのy方向の速度の変化は運動量保存則より、
\[V_{y}’-V_{y}=\frac{J_{t}}{M}\]
となる。体重が重いほど、ブレが少なくなり、回転をかければかけるほど、ブレが大きくなる。
衝突後ラケットのx方向の速度の変化は、式(8)のx成分を参照。体重が重いほど、ブレが少なくなる。